Задания и ответы для 7-8 классов олимпиады по математике пригласительный школьный этап всероссийской школьной олимпиады (ВОШ), официальная дата проведения олимпиады в режиме онлайн: 13.05.2020 (13 мая 2020 год) вариант 2.
Ссылка для скачивания всех классов: купить
Некоторые задания и ответы 7 класс пригласительный этап по Математике 2020-2021 (вариант 2):
№ 1. Денис загадал четыре различных натуральных числа. Он утверждает, что
— произведение наименьшего и наибольшего чисел равно 32;
— произведение двух оставшихся чисел равно 26.
Чему равна сумма всех четырёх чисел?
Ответ: 48
№ 2. Вдоль дороги стоят дома Андрея, Бори, Васи и Гены (именно в таком порядке). Расстояние между домами Андрея и Гены равно 2350 метрам. Однажды ребята решили устроить забег на 1 км. Они поставили старт на полпути от дома Андрея до дома Васи. При этом финиш оказался ровно на полпути от дома Бори до дома Гены. Чему равно расстояние от дома Бори до дома Васи? Ответ укажите в метрах.
Ответ: 350
№ 3. Числа 1, 2, 3, 5, 9, 10 расставили в клетки фигуры, изображённой на рисунке, так, чтобы суммы чисел во всех столбцах (включая столбец из одной клетки) были равны. Какое число может стоять в самой верхней клетке? Укажите все возможные варианты.
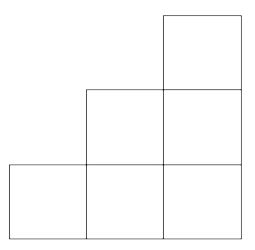
— 1
— 2
— 4
— 5
— 8
— 10
Ответ: 234
№ 4. В понедельник 4 человек из класса получили пятёрки по математике, во вторник пятёрки получили 8 человек, в среду — 5 человек, в четверг — 3 человека, в пятницу — 9 человек. Никто из учеников не получал пятёрки два дня подряд. Какое наименьшее количество учеников могло учиться в классе?
Ответ: 13
Некоторые задания и ответы 8 класс пригласительный этап по Математике 2020-2021 (вариант 2):
№ 1. Глеб расставил числа 1, 4, 5, 6, 8, 10, 14 в вершины и центр правильного шестиугольника так, что в любом из 6 равносторонних треугольников сумма чисел в вершинах делится на 3. Какое число Глеб мог записать в центр? Достаточно привести один подходящий пример.
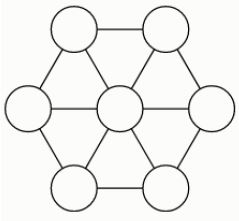Ответ: 6
№ 2. Миша предложил Юле передвинуть фишку из клетки A в клетку B. За один шаг можно передвинуть фишку в соседнюю по стороне или по углу клетку. Чтобы было интереснее, Миша положил 30 конфет в призовой фонд, но сказал, что будет забирать по 7 конфет за каждый горизонтальный или вертикальный ход и по 3 конфет за каждый диагональный ход. Оставшиеся конфеты Юля получает в награду. Какое максимальное количество конфет может выиграть Юля?
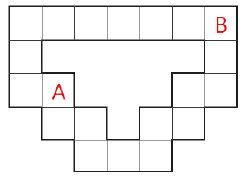Ответ: 14
№ 3. Учитель нарисовал на доске 4 таблицы 4×4. Он вызвал к доске Альберта, Богдана, Вадима и Дениса. Каждый из мальчиков выбрал себе одну таблицу. Альберт и Богдан просто закрасили некоторые клетки своих таблиц. Вадим закрасил на своей таблице только те клетки, которые были не закрашены и у Альберта, и у Богдана. Денис аналогично закрасил только те клетки, которые были не закрашены и у Богдана, и у Вадима. Мальчики сели на место, и учитель увидел на доске такие 4 таблицы. Помогите учителю определить, какая таблица кому принадлежит.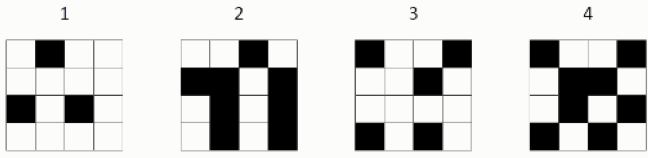
Для создания пары сперва нажмите на одну из строк левого столбца, а затем на необходимую строку в правом. Каждой строке в левом столбце соответствует ровна одна строка в правом.
| Алберт закрасил | 1 таблицу |
| Богдан закрасил | 2 таблицу |
| Вадим закрасил | 3 таблицу |
| Денис закрасил | 4 таблицу |
Ответ: 4213
№ 4. Диагонали четырёхугольника ABCD пересекаются в точке K. Оказалось, что AB=BK=KD. На отрезке KC отметили такую точку L, что AK=LC. Найдите ∠BLA, если известно, что ∠ABD=56∘ и ∠CDB=82∘.
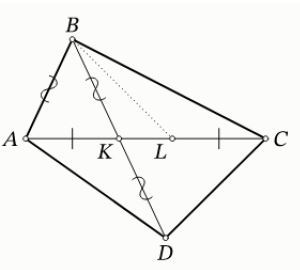Ответ: 30
Ссылка для скачивания всех классов: купить
* ВОШ (официальные материалы)
* Другие олимпиады и конкурсы
* Другие олимпиады и конкурсы